IOAA: The Sun
Contents
My notes to prepare Team USA for the solar portion of the 2021 IOAA.
Source: Carroll, Ostlie - chapter 11
Sun
- spectral class G2
Composition
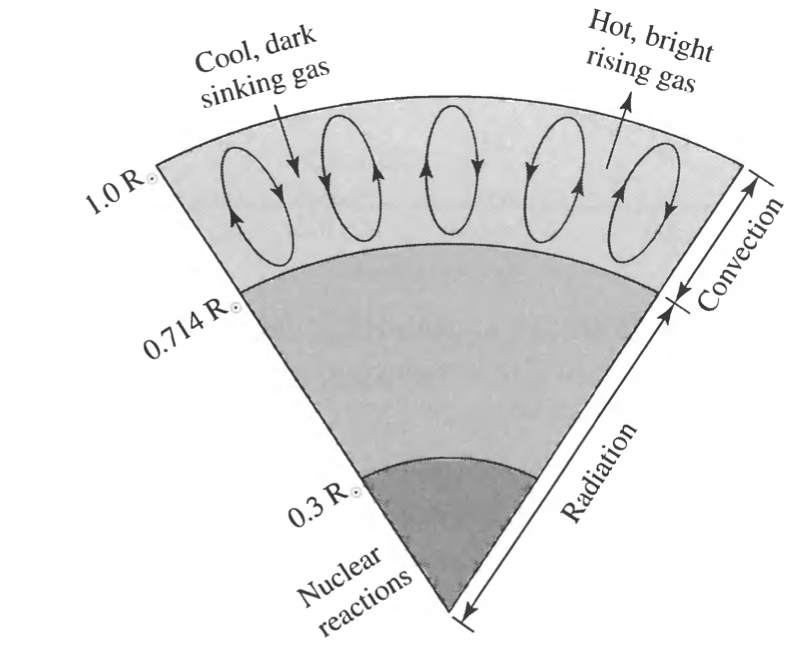
- Radiative core surrounded by a convective envelope
- Sun produces energy through the proton-proton chain
- Produces He^3^ as an intermediate (it’s created and then destroyed)
- He^3^ - He^3^ interactions require high temperatures
- At greater depths, these interactions result in He^3^ being destroyed faster, so it is less abundant there
- Explains the bump of He^3^ abundance at 0.3R
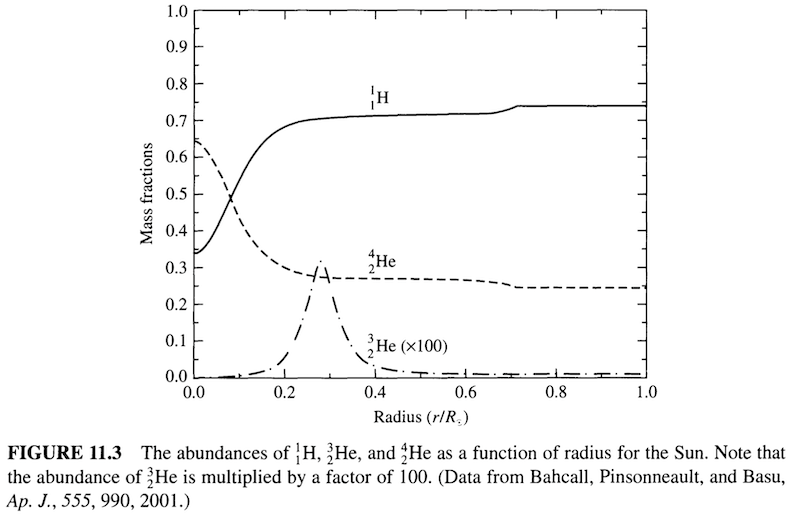
- Bump near 0.7R is explained by changes in position of base of the surface convection zone
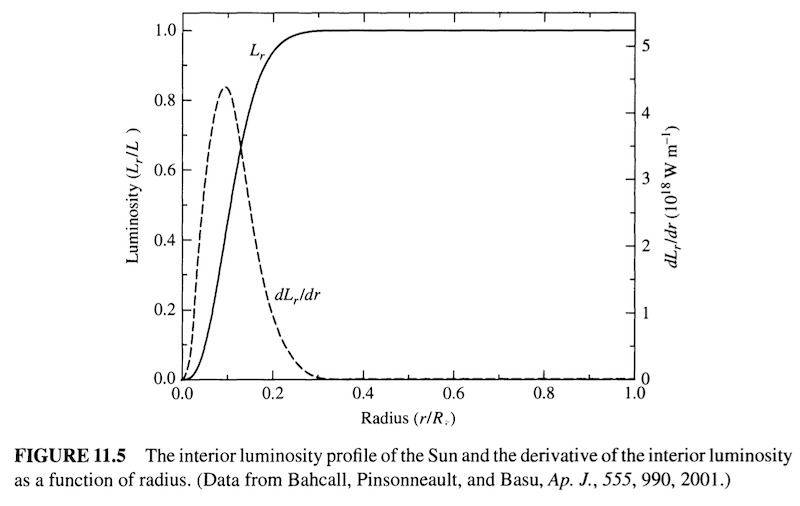
- Volume of shell is given by $dV = 4\pi r^2 dr$, so shells further away from the center have more mass
- On the other hand, going closer to the center of the sun, nuclear reactions happen more rapidly
- Hence, maximum energy production occurs at ~0.1R
Neutrino Problem
- “Neutrino problem” began when Raymond Davis measured neutrinos from the sun in the Homestake experiment
- Expected a rate of 7.9 SNU, observed a rate at 2.56 SNU
- 1 SNU = 1 solar neutrino unit = 10^-36^ reactions per target atom per second
- Discrepancy is explained by neutrino oscillation, where neutrinos change between 3 different flavors
- Electron, muon, tau flavors
- Implies that neutrino have mass
Solar Rotation
- Sun undergoes differential rotation - rate varies with latitude
- Solar rotation period…
- …at the equator = 24.47 days
- …at the poles = 38 days
- …on average = 28 days
Carrington Rotation (CR)
- Used to follow sunspots
- Approx. 25.38 (siderial period) or 27.2523 (synodic period)
Layers of the Sun

- tau_500 is the optical depth at 500 nanometers
Photosphere
- Region where the observed optical photons originate
- Effective temperature = temperature of the gas at this depth: T~e~ = T~τ=2/3~ = 5777 K
- Absorption lines (e.g. Fraunhofer lines) are produced here
- Contains granulation, a patchwork of bright and dark regions
Optical Depth
- Optical depth is defined as $\tau = -\ln(f)$, where $f$ is the fraction of photons originating from a layer that reach us.
- Alternatively, $e^{-\tau} = f$.
Example: if 1% of the photons from a layer reach us, the optical depth is 4.5, since $e^{-4.5} \approx 0.01$.
On average, the solar flux is emitted from an optical depth of 2/3 (Eddington approximation).
Sunspots
- Located in the photosphere
- Plot of sunspot location as a function of time creates Manuder’s butterfly diagram:
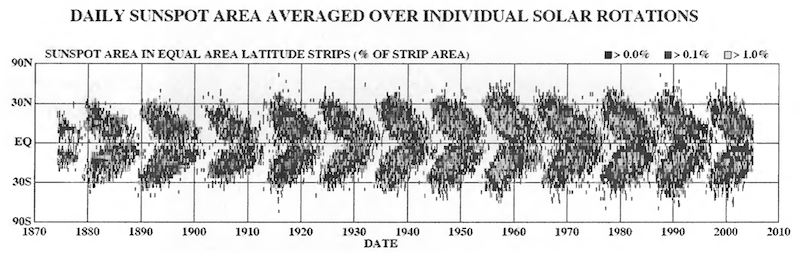
- Sunspots generally originate at 40 N and 40 S latitude
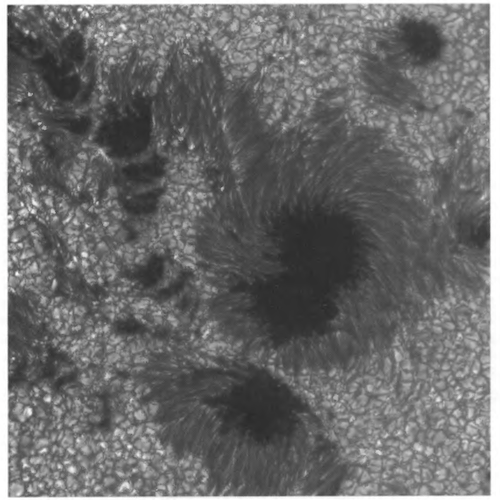

Dark central portion of sunspot = umbra
- Darker because sunspots are cooler (3900 K vs. surface temperature of 5700 K)
Lighter surrounding “filamental” region = penumbra
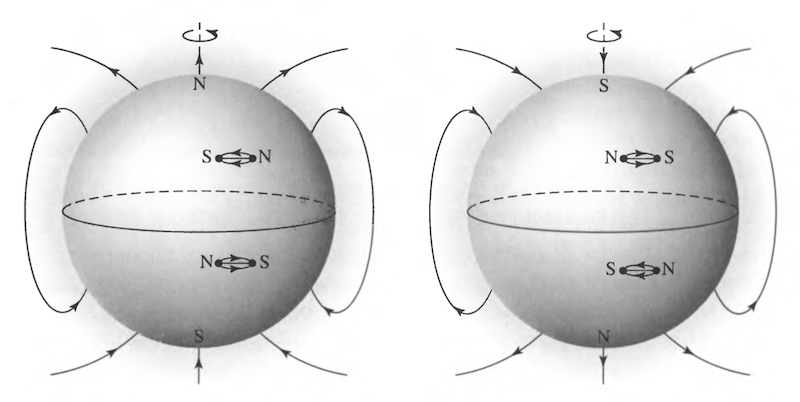
Sun’s polarity and the polarity of sunspots (location of magnetic north and south) flips every 11 years, so the sun is on a 22-year cycle
Chromosphere
- Portion that lies above the photosphere and extends upward for approx. 1600 km
- Density decreases and temperature increases with increasing altitude
- 6,000 K at the base to 35,000 K at the base of the corona
- Contains spicules, dynamic jets of plasma that appear as “hairs”
- Contains prominences, a large gas feature extending from the surface and often loops
- If it breaks, it releases a CME
- When viewed against the solar disk, it’s a filament
- When viewed from the side, it’s a prominence
Corona
- Extends above the chromosphere
- Extremely low density, effectively transparent to most radiation
- Temperatures in excess of 10^6^ K
Solar Wind
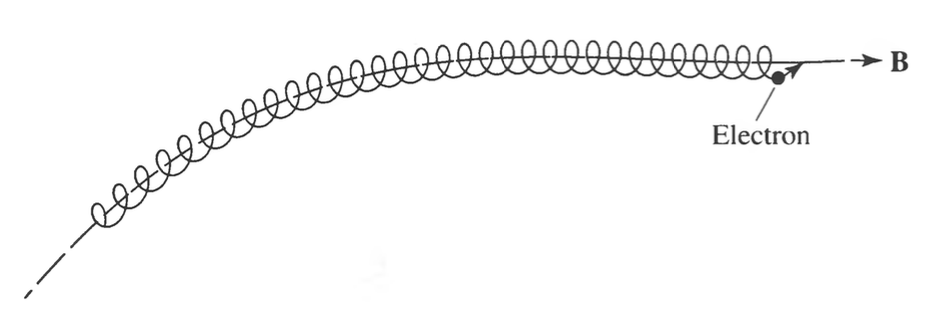
- Dark, cool regions known as coronal holes exist
- Correspond to parts of the magnetic field where the field lines are open
- This results in the solar field (particles can follow their way out of the sun due to lorentz force)
Radiation Pressure
- Magnetohydrodynamics (MHD) is the study of the interaction between magnetic fields and plasmas
Using MHD, we can show that the magnetic energy density $u_m$ and magnetic pressure $P_m$ are equal:
$$u_m = P_m = \frac{B^2}{2\mu_0}$$
Alfven Waves
- Disturbances in magnetic field lines can propgate down the line, creating an Alfven wave
- Adiabatic sound speed is given by $v_s = \sqrt{\gamma P_g/\rho}$, so the Alfven wave should be similiar.
- Careful analysis shows that Alfven wave speed is $v_m = B/\sqrt{\mu_0\rho}$
Solar Flares
- Events that release trememdous amounts of energy (10^17^ J to 10^25^ J) as well as charged particles
- Caused by reconnection of magnetic field lines
- Field lines break and reconnect, releasing energy
Coronal Mass Ejections
- 5 x 10^12^ kg to 5 x 10^13^ kg of mass is ejected from the corona during a CME
- Approximately 1 per day (max of 3.5/day during high solar activity, low of 0.2/day during low solar activity)